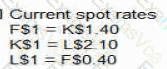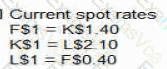Why not A?
For A:
Spot: F$1 = K$1.40
1-year forward: F$1 = K$1.44
Interest: F$ at 5%, K$ at 8%
Covered interest parity condition:
F=S×1+iK1+iFF = S \times \frac{1+i_{K}}{1+i_{F}}F=S×1+iF1+iK F=1.40×1.081.05=1.40×1.028571…≈1.44F = 1.40 \times \frac{1.08}{1.05} = 1.40 \times 1.028571… \approx 1.44F=1.40×1.051.08=1.40×1.028571…≈1.44
Forward rate is consistent with interest rates → no arbitrage.
Option D – Covered interest arbitrage
For D, everything is the same except K$ interest = 9%:
Fno-arbitrage=1.40×1.091.05=1.40×1.038095…≈1.45F_{\text{no-arbitrage}} = 1.40 \times \frac{1.09}{1.05} = 1.40 \times 1.038095… \approx 1.45Fno-arbitrage=1.40×1.051.09=1.40×1.038095…≈1.45
But given forward is only 1.44, so:
Borrow F$, convert to K$, invest at 9%, and lock in selling K$ forward at 1.44.
This produces a risk-free return greater than 5%, so covered interest arbitrage exists.
Option B vs C – Triangular arbitrage
From the first two quotes:
\text{F$1} = \text{K$1.40},\quad \text{K$1} = \text{L$2.10} \Rightarrow \text{F$1} = 1.40 \times 2.10 = \text{L$2.94}
So the implied rate is:
\text{L$1} = \frac{1}{2.94} \approx \text{F$0.3401}
Option B gives L$1 = F$0.34 → essentially equal (no exploitable difference assumed in exam context) → no arbitrage.
Option C gives L$1 = F$0.40, which is far from 0.3401 → direct L$/F$ quote is inconsistent with cross-rate ⇒ triangular arbitrage opportunity.
Answer: Options C and D offer arbitrage opportunities.